Урок 4
|
Позиционные системы счисления.
|
|||||||||||
Здравствуйте мои дорогие!
Ну вот и пришло время последнего урока в летнем семестре.
Начнем наш урок с небольшой шутки. Прочитайте стихотворение:
|
||||||||||||
Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила -
Все это правда, а не бред,
Когда пыля десятком ног,
Он шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз
Рассматривали мир привычно…
Но станет все совсем обычным,
Когда поймете наш рассказ.
А.Н.Стариков
«Необыкновенная девочка»
|
||||||||||||
Я думаю, вы уже догадались, в чем тут секрет. Просто все числа в этом стихотворении записаны не в десятичной, а в двоичной системе. Действительно, 1100 лет в двоичной системе - это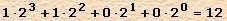
 лет в десятичной системе, а у щенка было  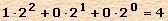лапы. Двоичная система самая простая, потому что для нее требуется меньше всего цифр - 0 и 1. В десятичной системе нужны 10 цифр (считая и 0), в пятеричной - 5 цифр, в восьмеричной - 8. На практике двоичная система мало удобна получаются слишком длинные числа. Но именно благодаря этой системе мы имеем такую «волшебную палочку», как компьютер.
Нетрудно сообразить, что в каждой системе высшая цифра, какая может понадобиться, равна основанию этой системы без единицы. Например, в десятичной системе высшая цифра 9, в шестеричной - 5, в шестнадцатеричной - 15 и т.д.
Переводить числа из одной системы в другую не сложно, но надо потренироваться. Попробуем записать число 119 в пятеричной системе. Сначала узнаем, сколько в нем единиц первого разряда:
119:5=23, остаток 4.
Значит число простых единиц будет 4. Далее, узнаем сколько будет единиц второго разряда:
23:5=4, остаток 3.
Это показывает, что во втором разряде («пятерок») будет цифра 3, а в третьем («двадцатипяте- рок») - 4.
Итак,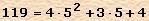
 , или в пятеричной системе «434». Описанные действия обычно записывают так:
 Подчеркнутые числа записывают справа налево и сразу получают изображение числа в другой
системе. Например, запишем число 1579 в двенадцатеричной системе:
 В системах с основанием больше 10 для записи цифр больше 9 обычно используют латинские
буквы A, B, С, D и т.д. Поэтому число 1579 в двенадцатеричной системе запишется так - АВ7. Проверим: 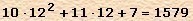 . А теперь попробуем выполнить арифметические действия в разных системах.
Например, сосчитать 2143-334, 213х3, 2402:31 в пятеричной системе.
Конечно, можно сначала изобразить написанные числа в десятичной системе, а результат перевести в пятеричную. Но лучше поступать иначе: составить «таблицу сложения» и «таблицу умножения» для той системы, которая нам требуется.
|
||||||||||||
Например таблица сложения для пятеричной системы такова:
|
||||||||||||
С помощью этой таблички мы легко сосчитаем:
 . |
||||||||||||
А таблица умножения (или «Пифагорова таблица»)
для пятеричной системы имеет вид: |
||||||||||||
Теперь считаем
|
||||||||||||
Конечно, самые простые таблицы для двоичной системы. Вот они:
 и  . То есть умножения в этой системе как бы и нет, а для сложения надо запомнить, что 1+1=10. Поэтому длиннота записи чисел искупается простотой выполнения арифметических операций.
Ну, вам осталось только не запутаться во всем этом.
Домашнее задание.
1. Запишите все числа из стихотворения в десятичной системе.
2. Напишите число 130 в нескольких системах, какие вам нравятся (от двоичной до шестнадцатеричной).
3. Составьте таблицы сложения и умножения для троичной системы и сосчитайте:
а) 212+120+201
б)
 в) 220:2
г) 201:12
4. В бумагах одного чудака найдена была его автобиография. Она начиналась следующими строками:
«Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте всего 11 лет способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей.»
Попробуйте разгадать ее.
Дополнительное задание.
Известно, что
121:11=11
144:12=12
 во всех системах счисления (где имеются соответствующие цифры).
Докажите это.
|
||||||||||||
Пожалуйста, присылайте не только ответы, но и решения.
Предупреждаю вас, что ответы на все уроки и переменки принимаются только до 17 августа.
Желаю успеха.
|
||||||||||||
 |
||||||||||||
Ответы присылайте
с Силантием
|
||||||||||||
